关国卉
中国人民大学统计学院,风险管理与精算讲
师。
研究领域
主要研究领域为保险精算、最优投资决策问
题、养老资金管理等。已有多篇论文发表于
保险精算顶尖期刊中,如《Insurance:
Mathematics and Economics》、
《Scandinavian Actuarial Journal》等。主
持多项基金,包括国家自科青年项目,博士
后面上基金等。

王晓军(通讯作者)
中国人民大学统计学院院长、教授、博士生导
师,中国人民大学杰出学者特聘教授,中国人
民大学-国家统计局数据开发中心执行主任,国
家社科基金重大项目首席专家,兼任SOA中国委
员会教育分委会主席,中华预防医学会健康保
险专业委员会副主任,中国保险学会常务理
事,入选教育部新世纪优秀人才、北京市新世
纪社科理论人才百人工程人才,享受国务院政
府特殊津贴,曾获北京市教育创新标兵,中国
人民大学十大教学标兵,北京市高等教育教学
成果一等奖等荣誉。
论文题目
Time-consistent reinsurance and investment strategies for an AAI under smooth ambiguity utility
英文摘要
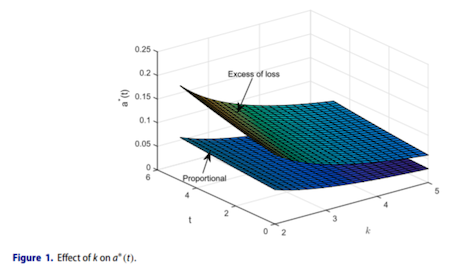
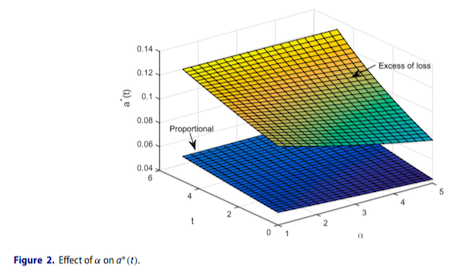
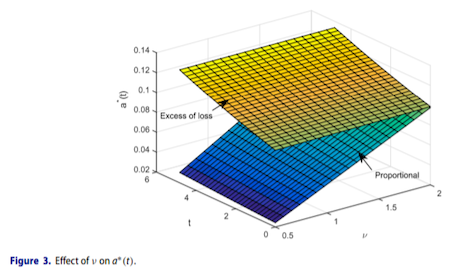
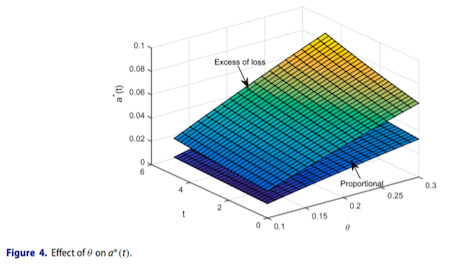
This paper investigates time-consistent reinsurance(excess-of-loss, proportional) and investment strategies for an ambiguity averse insurer(abbr. AAI). The AAI is ambiguous towards the insurance and financial markets. In the AAI`s attitude, the intensity of the insurance claims` number and the market price of risk of a stock can not be estimated accurately. This formulation of ambiguity is similar to the uncertainty of different equivalent probability measures. The AAI can purchase excess-of-loss or proportional reinsurance to hedge the insurance risk and invest in a financial market with cash and an ambiguous stock. We investigate the optimization goal under smooth ambiguity given in Klibanoff, P., Marinacci, M., & Mukerji, S. (2005), which aims to search the optimal strategies under average case. The utility function does not satisfy the Bellman`s principle and we employ the extended HJB equation proposed in Björk, T. & Murgoci, A. (2014) to solve this problem. In the end of this paper, we derive the equilibrium reinsurance and investment strategies under smooth ambiguity and present the sensitivity analysis to show the AAI`s economic behaviors.
中文摘要
本文研究模糊厌恶型保险公司的时间一致再保险(超额赔款再保险、比例再保险)和投资决策,保险公司对于保险市场和金融市场的认知带有不确定性,其中,保险赔付数量的强度和股票的收益率无法准确估计,我们通过不同的等价鞅测度刻画这种不确定性。保险公司可以购买再保险产品来管理保险风险、投资现金和权益管理市场风险,我们基于Klibanoff, P., Marinacci, M., 和Mukerji, S. (2005)中的光滑模糊构造保险公司的最优目标,在光滑模糊的框架下,效用函数不再满足贝尔曼原理,我们引入Björk, T. 和 Murgoci, A. (2014)中拓展的HJB方程进行求解,并得到了在光滑模糊效用下保险公司的均衡再保险和投资策略,最后通过数值模拟分析了保险公司的经济行为。
论文发表截图